해쉬테이블 🤔

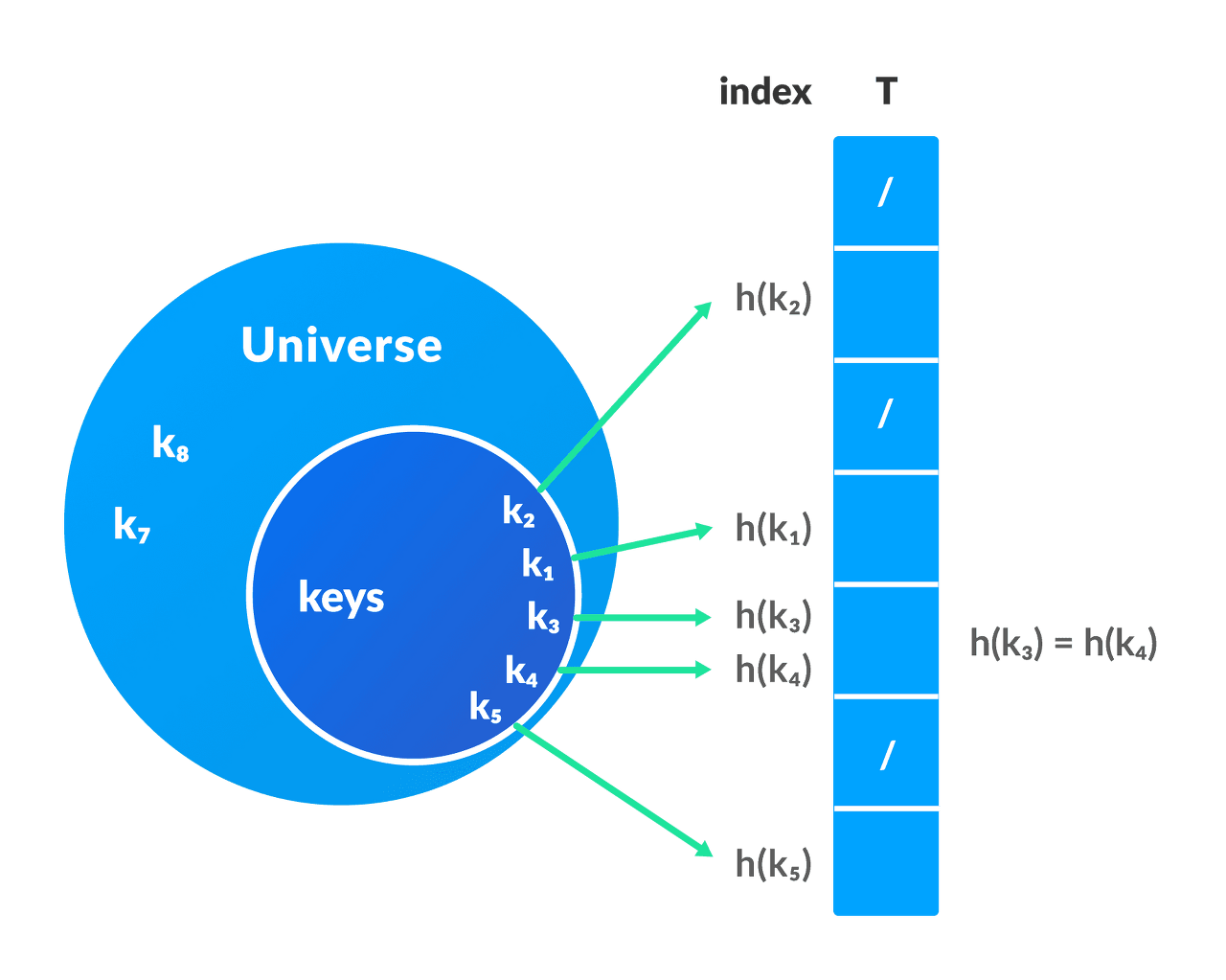
• 키에 데이터를 맵핑할 수 있는 데이터구조이다.
  • 키와 값을 어떻게 맵핑할까? → 해쉬 펑션에 키를 넣으면 키를 저장할 수 있는 주소를 리턴을 해준다.(인덱스) 해당 주소에 키에 해당하는 값을 저장한다.
  • 해시 펑션은 뭘까? → 임의의 데이터를 고정된 길이의 값으로 리턴해주는 함수이다. (데이터가 어떻든간에 고정된 길의의 값으로 리턴해준다.)
• 해쉬테이블에 저장한다면 어떤 키던간에 해시 펑션을 이용하면 해당 데이터의 위치를 리턴해주기 때문에 빠른 탐색 속도를 보여준다.
• 해쉬테이블 ⇒ 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
  • 슬롯 : 해쉬 테이블에서 한 개의 데이터를 저장할 수 있는 공간
• 전체적인 흐름 ? → 키와 데이터를 입력하면 해쉬 펑션은 입력된 키를 바탕으로 인덱스 번호를 반환해 해당 데이터가 저장될 수 있는 공간을 배열로 할당한 후, 키에 따른 데이터를 저장한다.
  • 탐색시에는 키를 입력하면 해쉬 펑션은 인덱스를 리턴해주기 때문에 불필요한 탐색을 할 필요 없이 데이터의 유무를 판단해 해당 인덱스의 데이터로 바로 접근이 가능하다.

해쉬 테이블의 장단점과 주요 용도 🤔

• 장점
  • 데이터 저장/읽기 속도가 빠르다.(처음부터 탐색할 필요 없이 해당 인덱스에 바로 접근이 가능하기 때문에)
  • 해쉬는 키에 대한 데이터가 있는지 확인이 쉽다.(중복 확인이 쉽다.)
• 단점
  • 일반적으로 저장 공간이 좀 더 많이 필요하다.
  • 여러 키에 해당하는 주소가 동일할 경우 충돌을 해결하기 위한 별도 자료구조가 필요하다.
• 주요 용도
  • 검색이 많이 필요한경우
  • 저장,삭제,읽기가 빈번한경우
  • 캐쉬 구현시 (중복 확인이 쉽기 때문이다.)

해쉬 충돌(컬리젼)을 위한 알고리즘 (키는 다르지만 해쉬 펑션으로 인한 반환값이 같을때) 🤔

체이닝 기법 (순회를 하기 때문에 시간이 좀 걸린다.)

• 개방 해슁 또는 오픈 해슁 기법중 하나이다. (해쉬 테이블 저장공간 외의 공간을 활용하는 기법 /그래서 오픈이라는 개념을 가진다.)
• 충돌이 일어나면 링크드 리스트를 사용해서 데이터를 추가로 뒤에 연결시켜서 저장한다.
• 기존의 슬롯에 키와 연결용 next 객체를 새로 멤버변수로 선언해준다.
• 이미 해당 슬롯이 있다면? 해당 슬롯을 참조하는 prevSlot / findSlot 객체를 생성해 key가 같다면 벨류 값을 바꾸고, 다르다면 순회를 하면서 null을 찾을때까지 포인터를 연결 후 새로 슬롯을 생성해 데이터를 저장한다.

리니어 프로빙 기법

• 폐쇄 해슁 기법중 하나이다. (해쉬 테이블 저장공간 안에서 충돌 문제를 해결하는 기법이다. / 해쉬 테이블 저장공간 안에서 해결을 하기 때문에 폐쇄 라는 용어가 붙는다.)
• 충돌이 일어나면 해당 해쉬 어드래스의 다음 어드래스부터 맨 처음 나오는 빈 공간에 저장하는 기법이다.
  • 저장공간 활용도를 높이기 위한 기법이다.
• 마찬가지로 key를 함께 저장한다.
• 해당 슬롯에 데이터가 존재한다면? 계속 뒤 인덱스로 순회를 하면서 null이 나올때까지 탐색 후 null이 존재하지 않는다면 저장을 하지 않는다.

해쉬 테이블 시간복잡도 🤔

• 일반적인 경우 (컬리젼이 없다면) O(1)
• 최악의 경우 (컬리전이 모두 발생하는 경우) O(n)
• 리니어 프로빙, 체이닝 기법 둘 다 동일하다.

해쉬 테이블의 경우는 일반적인 경우를 기대하고 작성한다.

검색에서 해쉬 테이블의 사용 예

• 배열에 데이털르 저장하고 검색할때는 O(n) 이지만 이상적인 해쉬 테이블 케이스에서 데이터를 검색할때는 O(1)이다. → 배열은 무조건 반복문을 이용하지만 해쉬 테이블은 해쉬펑션이 인덱스를 리턴해주기 때문에 O(1)이다.

마무리 🤔

• 단순히 아무생각없이 사용하던 해쉬맵이 이름과 밸류를 통으로 저장해버리는 줄 알았는데 기본 원리는 키는 해쉬펑션으로 인하여 인덱스를 반환해주면 밸류를 가져오지만, 충돌이 일어날 시에 대비하기 위해서 키도 같이 저장하는구나! 를 알게되었습니다.
• 해쉬 테이블이 어떻게 동작하는지 알 수 있게 되었습니다.
• 단순히 해쉬 테이블 자료구조를 사용하는 API를 이용하는것이 아니라 적절한 사용이 맞는지 판단해 최대한 충돌이 일어나지 않는 상황에서 해쉬 자료구조를 택한다면 좋은 성능을 발휘할 것 같습니다.
• 체이닝 기법, 리니어 프로빙 기법이 해쉬 충돌 해결방안 이긴 하지만 전체적으로 돌아가는 구조를 보니 그냥 충돌 자체가 안나는게 최적의 상황인것 같습니다. 자주 충돌이 날 수 있는 상황이라면 다른 자료구조를 사용하는게.. 🤔
• 적절한 해쉬 펑션을 어떻게 만드는지가 가장 중요한것 같습니다. 해당 부분에 대해서 공부할 필요가 있다고 느껴졌습니다.

알고리즘 복잡도 표현 방법 🤔

어떤 문제를 풀이하는데 완벽하게 똑같은 코드는 존재하지 않으나 어떤 풀이가 좋은 풀이냐 ? 라는 기준을 표현하는 방법을 익히는 것이다.

→ 어느 알고리즘이 더 좋은지를 분석하기 위해서 복잡도 라는 것을 정의 해 알고리즘 간에 비교를 한다.

어떻게 정의를 할까? 🤔

• 시간 복잡도⇒ 알고리즘의 실행 속도를 의미한다.
• 공간 복잡도⇒ 알고리즘이 사용하는 메모리 사이즈를 의미한다.

(사실상 공간 복잡도 보다는 시간 복잡도로 평가하는 경우가 많다.)

시간 복잡도는 어떻게 계산할까? 🤔

결과적으로는 반복문이 지배한다.

프로그래밍은 변수/조건문/반복문 으로 이루어져 있다.

이중 변수/조건문을 사용한다 해서 프로그램 성능을 좌우하진 않으나 반복문은 영향을 끼친다.

결과적으론 시간 복잡도에는 반복문이 큰 영향을 끼친다.

알고리즘 성능 표기법 🤔

• Big O (빅-오) 표기법 : O(n)
  • 알고리즘 최악의 실행 시간을 표기한다. (최악의 경우에 이 프로그램이 얼마의 시간이 걸릴것인가? 를 정의한다.)
  • 가장 많이 사용된다.
  • 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문이다.
• 오메가 표기법 : Ω(n)
  • 오메가 표기법은 알고리즘 최상의 실행 시간을 표기한다.
• 세타 표기법 : Θ(n)
  • 세타 표기법은 알고리즘 평균 실행 시간을 표기한다.

계산 표기는 최악의 시간인 빅오 표기법을 중심으로 익히면 된다.

빅 오 표기법 🤔

• 무조건 상수회 를 실행한다면 ? ⇒ O(1)
• 이중 반복문이지만 상위 (밖의 반복문이) 상수로 반복한다면 ? ⇒ O(n) (상수는 안쪽 반복문의 ~번(n)이 무한대가 되면 큰 의미가 없어진다.)
• 삼중 반복문이지만 상위가 상수번 반복한다면? O(n^2)

참고 → log n 의 베이스는 2-log2n 이다.

실질적으로 프로그램의 각각의 실행 속도는 다를 수 있지만 시간복잡도 비교는 이런식으로 가능하게 된다.

예제로 알아보자. 🤔

반복문으로 1부터 N까지의 합을 구하는 함수 ?

• 하나의 반복문이 사용된다.

하나의 반복문이기 때문에 무조건 상수회를 실행한다. 따라서 **O(1)**이라고 할 수 있다.

반복문으로 1부터 N까지의 합을 구하고 각 수 마다 또 다시 N까지의 숫자를 한번 더 더 한다면?

• 상수로 반복하는 반복문 안에 또 다른 반복문이 존재한다.

이중 반복문이지만 상위 반복문이 상수회 반복하기 때문에 **O(n)**이라 할 수 있다.

하지만 이중 반복문과 또 하나의 반복문이 나온다면?

3회 반복하는 반복문 안에 n번 실행하는 반복문이 2개가 존재하고 그 다음은 5회 반복하는 반복문안에 n번 실행하는 반복문이 하나가 존재한다면?

3n^2 + 5n 으로 표기하지 않고, 가장 높은 차수가 제일 중요하고 상수 자체는 큰 영향이 없기 때문에 빅오 표기법으로는 O(n^2)로 표기한다.

느낀점 🤔

• 시간복잡도에 대한 개념을 전혀 이해하지 못하고 알고리즘 문제를 풀이했었는데 굉장히 쉽게 이해가 되었습니다.
• 앞으로 알고리즘 문제를 풀때 시간초과가 날 수 있는 상황을 미리 예상하고 최적의 답을 입력할 수 있을것 같습니다.
• 뿐만 아니라 개발 할때도 적절한 상황에 적합한 코드를 작성하여 성능에도 신경 쓸 수 있겠구나 하는 생각이 들었습니다.🤔